Aljabar berasal dari kata algebra yang berarti ilmu menghitung dan cara penggunaan bilangan dengan huruf dan simbol, misalkan suku, faktor, koefisien, ko³nstanta, suku sejenis dan suku tak sejenis.bentuk-bentuk seperti 2a, -5b, x³, 3p + 2q disebut bentuk aljabar.
Pada bentuk aljabar 2a, 2 disebut koefisien, sedangkan a disebut variabel (peubah). Bentuk aljabar dapat digunakan untuk menyelesaikan permasalahan dalam kehidupan sehari hari, yang misalnya: untuk menghitung umur seseorang, menghitung banyaknya makanan yang dibutuhkan, dan permasalahan lainnya.
Variabel adalah lambang pengganti bila- ngan yang nilainya belum diketahui. Biasanya menggunakan x, y, a, b, dan seterusnya. Konstanta adalah suku di dalam aljabar yang tidak mempunyai variabel .
Koefisien
Koefisien adalah faktor konstanta dari suatu suku bentuk aljabar. Suku adalah variabel beserta koefisien dan konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah dan selisih. Suku dibedakan menjadi dua yaitu: suku sejenis dan suku tidak sejenis.
Suku Sejenis dan Suku Tidak Sejenis
Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.
Suku satu adalah bentuk aljabar yang tidak dihubungkan oleh operasi jumlah atau selisih.
Contoh: 3x, 2a², -4xy ...
Suku dua adalah bentuk aljabar yang dihubungkan oleh satu operasi jumlah atau selisih.
Contoh: 2x + 3, a² – 4, 3x² – 4x, ...
Suku tiga adalah bentuk aljabar yang dihubungkan oleh dua operasi jumlah atau selisih.
Contoh: 2x² – x + 1, 3x + y – xy, ...
Bentuk aljabar yang mempunyai lebih dari dua suku disebut suku banyak.
Catatan:
Bentuk aljabar suku dua disebut juga binom, bentuk aljabar suku tiga disebut trinom, sedangkan bentuk aljabar suku banyak disebut polinom.
Mengalikan bentuk aljabar
Perkalian suatu bilangan konstanta k dengan bentuk aljabar suku satu dan suku dua dinyatakan sebagai berikut:
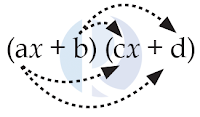
(ax + b) (cx + d) = ax × cx + ax × d + b × cx + b × d
= acx² + (ad + bc)x + bd
Menghitung operasi tambah, kurang, kali, bagi atau kuadrat bentuk aljabar
➧ Penjumlahan dan pengurangan (khusus pada suku sejenis = suku dengan variabel sama)
Sifat-sifat penjumlahan dan pengurangan yang berlaku pada bilangan riil, berlaku juga untuk penjumlahan dan pengurangan pada bentuk-bentuk aljabar, sebagai berikut:
Hasil bagi dua bentuk aljabar dapat kalian peroleh dengan menentukan terlebih dahulu faktor sekutu masing-masing bentuk aljabar tersebut, kemudian melakukan pembagian pada pembilang dan penyebutnya.
Untuk a bilangan riil dan n bilangan asli.
Dengan cara yang sama, bentuk (a – b)² juga dapat ditulis sebagai:
(a – b)² = (a – b) (a – b)
= (a – b)a + (a – b)(–b)
= a² – ab – ab + b²
= a² – 2ab + b²
Selanjutnya, akan diuraikan bentuk (a + b)³, sebagai berikut:
(a + b)³ = (a + b) (a + b)²
= (a + b) (a² + 2ab + b²) (a+b)²
= a² + 2ab + b²
= a(a² + 2ab + b² ) + b(a² + 2ab + b² )
= a³ + 2a²b + ab² + a²b + 2ab² + b³ (menggunakan cara skema)
= a³ + 2a²b + a²b + ab² +2ab² + b³ (suku yang sejenis dikelompokkan)
= a³ + 3a²b + 3ab² + b³ (operasikan suku-suku yang sejenis)
Untuk menguraikan bentuk aljabar (a + b)², (a + b)³, dan (a + b)⁴, kamu dapat menyelesaikannya dalam waktu singkat. Akan tetapi, bagaimana dengan bentuk aljabar (a + b)⁵, (a + b)⁶, (a + b)⁷, dan seterusnya? Tentu saja kamu juga dapat menguraikannya, meskipun akan memerlukan waktu yang lebih lama.
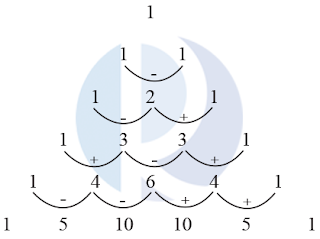
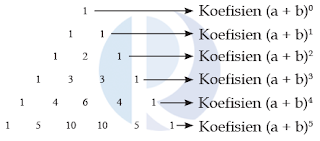
Untuk memudahkan penguraian perpangkatan bentuk-bentuk aljabar tersebut, kamu bisa menggunakan pola segitiga Pascal . Sekarang, perhatikan pola segitiga Pascal berikut:
Hubungan antara segitiga Pascal dengan perpangkatan suku dua bentuk aljabar adalah sebagai berikut:
Sebelumnya, kamu telah mengetahui bahwa bentuk aljabar (a + b)² dapat diuraikan menjadi a² + 2ab + b². Jika koefisien-koefisiennya dibandingkan dengan baris ketiga pola segitiga Pascal, hasilnya pasti sama, yaitu 1, 2, 1. Ini berarti, bentuk aljabar (a + b)2 mengikuti pola segitiga Pascal. Sekarang, perhatikan variabel pada bentuk a² + 2ab + b². Semakin ke kanan, pangkat a semakin berkurang (a² kemudian a).
Koefisien
Koefisien adalah faktor konstanta dari suatu suku bentuk aljabar. Suku adalah variabel beserta koefisien dan konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah dan selisih. Suku dibedakan menjadi dua yaitu: suku sejenis dan suku tidak sejenis.
Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.
Suku-suku sejenis adalah suku yang memiliki variabel dan pangkat dari masing-masing variabel yang sama.
Contoh:
5x dan -2x, 3a² dan 3a² dan a², y dan 4y,
Suku tak sejenis adalah suku yang memiliki variabel dan pangkat dari masing-masing variabel yang tidak sama.
Contoh:
2x dan -3x², -y dan –x³, 5x dan -2y, ....
Contoh:
5x dan -2x, 3a² dan 3a² dan a², y dan 4y,
Suku tak sejenis adalah suku yang memiliki variabel dan pangkat dari masing-masing variabel yang tidak sama.
Contoh:
2x dan -3x², -y dan –x³, 5x dan -2y, ....
Suku satu adalah bentuk aljabar yang tidak dihubungkan oleh operasi jumlah atau selisih.
Contoh: 3x, 2a², -4xy ...
Suku dua adalah bentuk aljabar yang dihubungkan oleh satu operasi jumlah atau selisih.
Contoh: 2x + 3, a² – 4, 3x² – 4x, ...
Suku tiga adalah bentuk aljabar yang dihubungkan oleh dua operasi jumlah atau selisih.
Contoh: 2x² – x + 1, 3x + y – xy, ...
Bentuk aljabar yang mempunyai lebih dari dua suku disebut suku banyak.
Catatan:
Bentuk aljabar suku dua disebut juga binom, bentuk aljabar suku tiga disebut trinom, sedangkan bentuk aljabar suku banyak disebut polinom.
Catatan:
Ingat bahwa untuk sebarang bilangan bulat a dan b, berlaku:
a × b = ab
a × (–b) = –ab
(–a) × b = –ab
(–a) × (–b) = ab
Ingat bahwa untuk sebarang bilangan bulat a dan b, berlaku:
a × b = ab
a × (–b) = –ab
(–a) × b = –ab
(–a) × (–b) = ab
Perkalian suatu bilangan konstanta k dengan bentuk aljabar suku satu dan suku dua dinyatakan sebagai berikut:
k (ax) = kax
k (ax + b) = kax + kb
k (ax + b) = kax + kb
= acx² + (ad + bc)x + bd
Selain skema di atas untuk mengalikan aljabar suku dua dengan suku dua dapat digunakan sifat distributif seperti uraian berikut:
(ax + b) + (cx + d) = ax (cx + d) + b (cx + d)
= ax × cx + ax × d + bcx + bd
= acx² + adx + bcx + bd
= acx² + (ad + bc)x + bd
(ax + b) + (cx + d) = ax (cx + d) + b (cx + d)
= ax × cx + ax × d + bcx + bd
= acx² + adx + bcx + bd
= acx² + (ad + bc)x + bd
➧ Penjumlahan dan pengurangan (khusus pada suku sejenis = suku dengan variabel sama)
Sifat-sifat penjumlahan dan pengurangan yang berlaku pada bilangan riil, berlaku juga untuk penjumlahan dan pengurangan pada bentuk-bentuk aljabar, sebagai berikut:
- Sifat Komutatif, a + b = b + a, dengan a dan b bilangan riil
- Sifat Asosiatif, (a + b) + c = a + (b +c), dengan a, b, dan c bilangan riil
- Sifat Distributif, a (b + c) = ab + ac, dengan a, b, dan c bilangan riil.
Hasil bagi dua bentuk aljabar dapat kalian peroleh dengan menentukan terlebih dahulu faktor sekutu masing-masing bentuk aljabar tersebut, kemudian melakukan pembagian pada pembilang dan penyebutnya.
➧ Perpangkatan bentuk aljabar
Bilangan berpangkat didefinisikan sebagai berikut:
Definisi bilangan berpangkat berlaku juga pada bentuk aljabar. Untuk lebih jelasnya, pelajari uraian berikut:
a5 = a × a × a × a × a
(2a)³ = 2a × 2a × 2a
= (2 × 2 × 2) × (a × a × a)
= 8a³
(–3p)⁴ = (–3p) . (–3p) × (–3p) × (–3p)
= ((–3) × (–3) × (–3) × (–3)) × (p × p × p × p)
= 81p⁴
(4x²y)² = (4x2y) x (4x2y)
= (4 × 4) × (x² × x²) × (y × y)
= 16x4y²
Sekarang, bagaimana dengan bentuk (a + b)²?
Bentuk (a + b)² merupakan bentuk lain dari (a + b) (a + b).
Jadi, dengan menggunakan sifat distributif, bentuk (a + b)² dapat ditulis:
(a + b)² = (a + b) (a + b)
= (a + b)a + (a + b)b
= a² + ab + ab + b²
= a² + 2ab + b²
a5 = a × a × a × a × a
(2a)³ = 2a × 2a × 2a
= (2 × 2 × 2) × (a × a × a)
= 8a³
(–3p)⁴ = (–3p) . (–3p) × (–3p) × (–3p)
= ((–3) × (–3) × (–3) × (–3)) × (p × p × p × p)
= 81p⁴
(4x²y)² = (4x2y) x (4x2y)
= (4 × 4) × (x² × x²) × (y × y)
= 16x4y²
Sekarang, bagaimana dengan bentuk (a + b)²?
Bentuk (a + b)² merupakan bentuk lain dari (a + b) (a + b).
Jadi, dengan menggunakan sifat distributif, bentuk (a + b)² dapat ditulis:
(a + b)² = (a + b) (a + b)
= (a + b)a + (a + b)b
= a² + ab + ab + b²
= a² + 2ab + b²
Dengan cara yang sama, bentuk (a – b)² juga dapat ditulis sebagai:
(a – b)² = (a – b) (a – b)
= (a – b)a + (a – b)(–b)
= a² – ab – ab + b²
= a² – 2ab + b²
Selanjutnya, akan diuraikan bentuk (a + b)³, sebagai berikut:
(a + b)³ = (a + b) (a + b)²
= (a + b) (a² + 2ab + b²) (a+b)²
= a² + 2ab + b²
= a(a² + 2ab + b² ) + b(a² + 2ab + b² )
= a³ + 2a²b + ab² + a²b + 2ab² + b³ (menggunakan cara skema)
= a³ + 2a²b + a²b + ab² +2ab² + b³ (suku yang sejenis dikelompokkan)
= a³ + 3a²b + 3ab² + b³ (operasikan suku-suku yang sejenis)
Untuk menguraikan bentuk aljabar (a + b)², (a + b)³, dan (a + b)⁴, kamu dapat menyelesaikannya dalam waktu singkat. Akan tetapi, bagaimana dengan bentuk aljabar (a + b)⁵, (a + b)⁶, (a + b)⁷, dan seterusnya? Tentu saja kamu juga dapat menguraikannya, meskipun akan memerlukan waktu yang lebih lama.
Sebaliknya, semakin ke kanan pangkat b semakin bertambah (b kemudian b²). Jadi, dengan menggunakan pola segitiga Pascal dan aturan perpangkatan variabel, bentuk-bentuk perpangkatan suku dua (a + b)³, (a + b)⁴, (a + b)⁵, dan seterusnya dapat diuraikan sebagai berikut:
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b3 + 5ab⁴ + b⁵
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b3 + 5ab⁴ + b⁵
Bantu Berikan DONASI jika artikel ini dirasa bermanfaat
Donasi akan digunakan untuk memperpanjang domain www.raimondwell.com
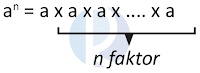
Terima Kasih telah meninggalkan komentarnya