Himpunan adalah kumpulan benda atau objek yang ciri-cirinya jelas, sehingga dengan tepat dapat diketahui objek yang termasuk himpunan dan yang tidak termasuk dalam himpunan tersebut. Suatu himpunan dilambangkan dengan huruf kapital A, B, C, D, E, …………….. Z, benda atau objek yang termasuk kedalam himpunan disebut a,nggota himpunan atau elemen himpunan ditulis dengan sepasang kurung kurawal {……..}
Huruf kapital yang digunakan untuk lambang himpunan tertentu:
Huruf A : Lambang Bilangan Asli,
A = {1,2,3,4,……}
Huruf B : Lambang Bilangan Bulat,
B = {….,-3,-2,-1,0,1,2,…..}
Huruf C : Lambang Bilangan Cacah,
C = {0,1,2,3,4}
Huruf Q : Lambang Bilangan Rasional.
Huruf A : Lambang Bilangan Asli,
A = {1,2,3,4,……}
Huruf B : Lambang Bilangan Bulat,
B = {….,-3,-2,-1,0,1,2,…..}
Huruf C : Lambang Bilangan Cacah,
C = {0,1,2,3,4}
Huruf Q : Lambang Bilangan Rasional.
Himpunan dapat dinyatakan melalui tiga cara:
- Dengan kata-kata, yaitu dengan menyebutkan semua syarat atau sifat-sifat keanggotaan dari suatu himpunan. Contoh: A adalah himpunan bilangan asli antara 5 dan 12, ditulis A = {bilangan asli antara 5 dan 12}
- Dengan Notasi Pembentuk Himpunan, yaitu menyebutkan semua syarat atau sifat ke-anggotaan dari suatu himpunan, tetapi anggota himpunan dinyatakan dalam variabel peubah. Contoh: A adalah himpunan bilangan asli antara 5 dan 12, dituliskan {x: 5<x<12,x bilangan asli}.
- Dengan Mendaftar Anggota-anggotanya, Yaitu menuliskan anggota-anggota himpunan dalam pasangan kurung kurawal dan memisahkan dengan tanda koma. Contoh: A adalah himpunan bilangan asli antara 5 dan 12, ditulis A= {6,7,8,9,10,11}
Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.
Simbol-simbol khusus yang dipakai dalam teori himpunan adalah:
Suatu himpunan dapat dinyatakan dengan tiga cara, yaitu dengan kata-kata, dengan notasi pembentuk himpunan, dan dengan mendaftar anggota-anggotanya.
Himpunan yang memiliki banyak anggota berhingga disebut himpunan berhingga. Himpunan yang memiliki banyak anggota tak berhingga disebut himpunan tak berhingga.
- Himpunan A merupakan himpunan bagian B, jika setiap anggota A juga menjadi anggota B dan dinotasikan
- Himpunan A bukan merupakan himpunan bagian B, jika terdapat anggota A yang bukan anggota B dan dinotasikan
- Setiap himpunan A merupakan himpunan bagian dari himpunan A sendiri, ditulis .
- Banyaknya semua himpunan bagian dari suatu himpunan adalah, dengan n banyaknya anggota himpunan tersebut
- Himpunan Semesta, himpunan semesta atau semesta pembicaraan adalah himpunan yang memuat semua anggota atau objek himpunan yang dibicarakan. Himpunan semesta (semesta pembicaraan) biasanya dilambangkan dengan S. Himpunan semesta adalah himpunan yang anggotanya semua objek pembicaraan. Himpunan semesta dilam-bangkan dengan S atau ⋃. Contoh: Kalau kita membahas mengenai 1, ½, -2, -½,… maka semesta pembicaraan kita adalah bilangan real. Jadi himpunan semesta yang dimaksud adalah R. Apakah hanya R saja? Jawabannya tidak. Tergantung kita mau membatasi pembicaraanya. Pada contoh di atas bisa saja dikatakan semestanya adalah C (himpunan bilangan kompleks). Namun kita tidak boleh mengambil Z (himpunan bilangan bulat) sebagai semesta pembicaraan. (Mengapa?).
- Himpunan Kosong, himpunan kosong adalah himpunan yang tidak mempunya anggota, dan dinotasikan dengan {} atau ∅. Himpunan nol adalah himpunan yang hanya mempunyai l anggota, yaitu nol (0).
- Himpunan Bagian, Himpunan A merupakan himpunan bagian B, jika setiap anggota A juga menjadi anggota B dan dinotasikan A ⊂ B atau B ⊃ A.
Jadi, A ⊂ B jika dan hanya jika 𝑥 ⊂ A ⇒ 𝑥 ⊂ B
Jika ada anggota dari A yang bukan merupakan anggota B, maka A bukan bukan himpunan bagian dari B, dilambangkan dengan A ⊄ B.
Contoh:
A = {1,3,5} dan B = {0,1,2,3,4,5,6}. Maka A ⊂ B.
C = {a,b,c,1,2} dan B = {0,1,2,3,4,5,6}.
Maka C ⊂ B, karena ada anggota dari C yang bukan merupakan anggota B, yaitu a. (Pengertian “ada” berarti terdapat satu anggota C yang bukan merupakan anggota B, sudah cukup)
Suatu himpunan pasti merupakan subset diri- nya sendiri. Jadi H ⊂ H.
Bukti:
Ambil sembarang h H, maka jelas h H.
Jadi H ⊂ H.
Himpunan kosong (∅) merupakan himpunan bagian dari semua himpunan.
Bukti:
Kalimat “𝑥 A ⇒ 𝑥 B” pada pengertian himpunan bagian (lihat definisi diatas), selalu bernilai benar jika diambil A = ∅ dan untuk sebarang himpunan B. Hal ini disebabkan syarat cukupnya selalu tidak terpenuhi. Sama saja dengan kita mengatakan “jika bulan bisa ngomong, maka dia tak akan bohong”. Kalimat ini selalu bernilai benar karena syarat cukupnya yaitu “bulan bisa ngomong” selalu tidak terpenuhi. Lebih lanjut mengenai hal ini akan dibicarakan dalam pembahasan mengenai LOGIKA
Diagram Venn pertama kali diketemukan oleh John Venn, seorang ahli matematika dari Inggris yang hidup pada tahun 1834–1923. Dalam diagram Venn, himpunan semesta dinyatakan dengan daerah persegi panjang, sedangkan himpunan lain dalam semesta
Untuk menyatakan suatu himpunan dapat dilakukan dengan:
- Menggunakan kata-kata,
- Mendaftar anggotanya, dan
- Menggunakan notasi pembentuk himpunan.
Berikut ini akan kita pelajari bagaimana menyatakan suatu himpunan dengan menggunakan gambar/diagram yang disebut dengan diagram Venn. Ketentuan dalam membuat diagram Venn adalah sebagai berikut:
Himpunan semesta digambarkan dengan sebuah persegi panjang dan di pojok kiri atas diberi simbol S. Setiap anggota himpunan semesta ditunjukkan de- ngan sebuah noktah/titik di dalam persegi panjang ter- sebut, dan nama anggotanya ditulis berdekatan dengan noktah/titik.
Contoh:
S = {1, 2, 3, 4, 5, 6, 7, 8}
Setiap himpunan yang termuat di dalam himpunan semesta ditunjukkan oleh kurva tertutup sederhana.
Himpunan semesta digambarkan dengan sebuah persegi panjang dan di pojok kiri atas diberi simbol S. Setiap anggota himpunan semesta ditunjukkan de- ngan sebuah noktah/titik di dalam persegi panjang ter- sebut, dan nama anggotanya ditulis berdekatan dengan noktah/titik.
Contoh:
S = {1, 2, 3, 4, 5, 6, 7, 8}
Setiap himpunan yang termuat di dalam himpunan semesta ditunjukkan oleh kurva tertutup sederhana.
Contoh:
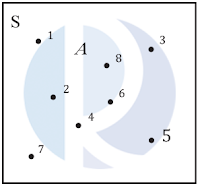
S = {1, 2, 3, 4, 5, 6, 7, 8}
A = {2, 4, 6, 8}
Karena semua anggota himpunan A termuat di dalam himpunan S, maka A berada dalam himpunan S
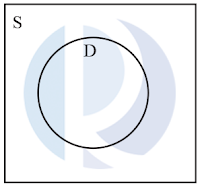
Dalam menggambar himpunan-himpunan yang mempunyai anggota banyak, pada diagram Venn tidak menggunakan noktah/titik.
Contoh:
S = {siswa di sekolah}
D = {siswa dalam kelas VII}
Irisan Himpunan
Perhatikan himpunan-himpunan berikut ini,
A = {a, b, c}
B = {a, b, c, d, e}
Dari kedua himpunan tersebut, ternyata setiap anggota A menjadi anggota B. Maka dapat dikatakan bahwa A adalah himpunan bagian dari B. Menggambarkannya dengan menggunakan diagram Venn adalah seperti berikut:
Berdasarkan diagram Venn tersebut di atas, himpunan A termuat di dalam himpunan B. Dari pembahasan di atas dapat disimpulkan bahwasanya himpunan A merupakan himpunan bagian dari B, bila setiap anggota A menjadi anggota B, ditulis dengan notasi A ⊂ B.
A = {2, 4, 6, 8}
Karena semua anggota himpunan A termuat di dalam himpunan S, maka A berada dalam himpunan S
Dalam menggambar himpunan-himpunan yang mempunyai anggota banyak, pada diagram Venn tidak menggunakan noktah/titik.
Contoh:
S = {siswa di sekolah}
D = {siswa dalam kelas VII}
Irisan Himpunan
Perhatikan himpunan-himpunan berikut ini,
A = {a, b, c}
B = {a, b, c, d, e}
Dari kedua himpunan tersebut, ternyata setiap anggota A menjadi anggota B. Maka dapat dikatakan bahwa A adalah himpunan bagian dari B. Menggambarkannya dengan menggunakan diagram Venn adalah seperti berikut:
Berdasarkan diagram Venn tersebut di atas, himpunan A termuat di dalam himpunan B. Dari pembahasan di atas dapat disimpulkan bahwasanya himpunan A merupakan himpunan bagian dari B, bila setiap anggota A menjadi anggota B, ditulis dengan notasi A ⊂ B.
Dari diagram Venn tersebut juga dapat dikatakan bahwa himpunan B memuat A, ditulis dengan notasi B ⊃ A.
A ⊂ B dibaca A himpunan bagian dari B
B ⊃ A dibaca B memuat A
Bantu Berikan DONASI jika artikel ini dirasa bermanfaat
Donasi akan digunakan untuk memperpanjang domain www.raimondwell.com












Terima Kasih telah meninggalkan komentarnya